Selection of Best Crop Under Uncertainty in Agriculture
0 Views
K. GURUCHARAN*, G. TEJASWINI REDDY, R. SHAFIYA AND P. LAVANYA KUMARI
Department of Statistics and Computer Applications, S.V. Agricultural College, ANGRAU, Tirupati
ABSTRACT
Decision making process involves selecting the best among several decisions through a proper evaluation of the parameters of each decision environment. An attempt is made under uncertainty conditions by nature of the farmer. This study is not only introduces concepts, principles and approaches for addressing uncertainty in decision making but also gives overview regarding practical method for modelling decisions under uncertainty and selecting decision alternatives that optimise the decision maker’s objectives. A farmer who followed multiple cropping system containing crops Groundnut, Paddy, Sunflower, Red gram, Cotton and Sesame. For that I have taken two factors i.e. production and price. From that I have drawn four variables i.e. good yield; high price, good yield; low price, poor yield; good price and poor yield; low price. Different methods were fitted to the data. If the farmer is optimistic, redgram is the best alternative under MAXIMAX criterion. If the farmer is pessimistic, Paddy is the best alternative as per MAXIMIN criterion. If the farmer is mixture of optimism and pessimism, redgram is best alternative as per HURWICZ criterion. If farmer considers always opportunity cost, sesame is best alternative as per SAVAGE MINIMAX REGRET criterion. If farmer considers the instances of each and every situation any event may occur in equal chance, Groundnut is the best alternative as per LAPLACE criterion. Based on this study farmer can rely for which crop to be taken for the next year based on the current production, prices and his behaviour irrespective of other factors.
KEYWORDS: HURWICZ, LAPLACE, MAXIMAX, MAXIMIN, Uncertainty
INTRODUCTION
The risk and uncertainty behaviour of decision makers have been well equipped with respect to individual agricultural producers. The terms ‘risk’ and ‘uncertainty’ can be defined in different ways. The major common difference is to suggest that risk is imperfect knowledge where the probabilities of the possible outcomes are known whereas uncertainty exists when these probabilities are not known.
A study on optimum allocation of agricultural land to the vegetable crops under uncertain profits usingfuzzy multi-objective linear programming-revealed the at optimum cropping pattern susing Linear Programming (LP) technique in case of fixed prices (profits) of crops. But instability in prices is high for vegetable crops due to their costly cultivation with high risk of profitability even though enhanced profits over food crops. This study makes an effort to compute the volatility in profits of vegetable crop sussing max-min approach of fuzzy programming. Results showed that the proper land utilization and proper cropping pattern is needed at farmers level itself. The farmer must grow the vegetable cropsin a way that it should be picked and be marketed in whole period to find at least best weighted return as an assured profit of 10.89 lakhs in spite of fluctuating prices (Kumari et al., 2014).
Ahuja (2010) defined risk as a situation in which the outcome of a decision is uncertain, but the probability of each possible outcome is known and can be estimated.In farming, many farm management decisions can be taken with no need to take explicit account of the risks involved. But some risky farm decisions will warrant giving more attention to the choice among the available alternatives.
Mostly in the agriculture sector, profit or loss are influenced by demand, supply, price of a crop, cost of cultivation etc. Sothe maximization of profit became a multi objective decision-making problem with unstable choices. Agricultural production is biological in nature and highly depends on agro-climatic conditions and is being carried out in small or medium sized farms. Therefore, the farmer must make decisions in extremely unstable and insecure circumstances (Nieuwoudt, 1972). Hence this study is taken up to give some hope and scope for the farming community. With decisions under uncertainty occur agroclimatic conditions (favourable/ moderately favourable/unfavourable), market price (good/average/poor), production (high/average/low) and pest instances (high/average/low)etc.
Sahin et al. (2008) determine the cattle fattening breed, which maximizes the net profit for the producers under risk and uncertainties. The Wald’s, Hurwicz’s, Maximax, Savage’s, Laplace’s and Utility criterions were used. On the other hand, the decision on which crops to include in crop rotation is one of the most important decisions in field crop farm management. Agronomic, economic and market information about each individual crop constitutes an informative basis for decision-making. There is a significant amount of valuable agronomic and market information already available on main crop production, including oil crops (Rozman et al., 2006). However, the potential for a wider range of alternative crops, including oil pumpkin (Bavec and Bavec, 2006), should be evaluated in order to determine their breakcrop characteristics and the benefits and challenges which they bring to systems (Robson et al., 2002).
Raju et al. (2000) studied on optimum cropping pattern for Sriramsagar project with an objective of maximization of net benefits. Uncertainty in the inflows arising out in the uncertainty in the rainfall is tackled through chance stochastic programming. Inflows at 4 levels of dependability viz., 75.00, 80.00, 85.00 and 90.00 per cent were considered in this study to obtain various possible optimal cropping patterns and optimal operating policies. Results indicated that for 90.00 per cent dependability level, paddy 450 (summer) and paddy (winter) occupied 62,930 ha and 14,700 ha area, respectively.
Frank and Ragnar (1999), emphasized that firm behaviour under risk with the help of panel data set of Norwegian salmon farms, showed that the structure of production risk plays an important role in production decisions of risk-averse producers, both with respect to optimal input levels and to adoption of new technologies. Farms are heterogeneous with respect to production risk. In other words, farms employing the same input levels have different levels of output risk. Inputs are found to be risk-controlling instruments. Since production risk is an inherent feature of the production process in most primary industries Bowden et al. (1985) explained the research paradigm for system agriculture. According to them, agriculture was a complicated human activity involving gun certainty and change. There was a need for system thinking considering agriculture with a sense of its complex wholesomeness and to take active and feasible action. According to them, Farming System Research was primarily concerned with the adoption of existing agricultural research to provide technology, relevant to farm resources.
MATERIAL AND METHODS
Let Di be the set of crops or decision alternatives or strategies (for i = 1, 2,3., m). E be the set of situations or events Ej (for j = 1, 2, 3., n) Rij be the set of payoffs (net returns) obtained by choosing crop Di if state Ej occurs.
1. Maximax Criterion
It is also known as the criterion of optimism, is used when the decision-maker is optimistic about future. Maximum payoffs is identified and the corresponding alternative is selected.
Maximax criterion (optimism)
Maximax criterion = Max (max Rij)
2. Maximin Criterion
It is also known as the criterion of pessimism, is used when the decision-maker is pessimistic about future. Maximin criterion implies the maximisation of the minimum payoff. The pessimistic decision-maker locates the minimum payoff for each possible alternative. The maximum of these minimum payoffs is identified and the corresponding alternative is selected.
Maximin criterion/Wald’s criterion(pessimism)
Maximin criterion = Max (min Rij)
3. Hurwicz Criterion
The approach would be to take into account the degree or index of optimism or pessimism of the decision- maker in the process of decision-making. If degree of optimism is a, a constant lying between 0 and 1and the degree of pessimism will be 1-a. Then a weighted average of the maximum and minimum payoffs of an action with a and 1-a as respective weights is computed. The action with the highest average is regarded as optimal.
We know a nearer to unity indicates that the decision- maker is optimistic while a value nearer to zero evidents the decision maker is pessimistic.
Hurwicz’s criterion
(Hi) =(maximum pay off)+ 1-a (minimum pay off) Hi = a (row maximum) + (1 – a) (row minimum) –
for positive payoffs (profits, revenues)
Hi= a (row minimum) + (1 – a) (row maximum) – for negative payoffs (costs, losses)
Best strategy will be Max { Hi } for positive payoffs, and Min { Hi } for negative payoffs.
1. Regret Criterion
Regret is the difference, which measures the magnitude of the loss incurred by not selecting the best alternative, is also known as opportunity loss or the opportunity cost.
Minimax regret criterion (savage’s criterion)
Regrets = Maximum payoff- payoff Minmax regrets = Min (maximum regrets)
2. Laplace Criterion
In the absence of any knowledge about the probabilities of occurrence of various states of nature, one possible way out is to assume that all of them are equally likely to occur. Using these probabilities, we compute the expected payoff for each course of action
and the action with maximum expected value is regarded as optimal.
Laplace criterion / equal probability/ Rationality/ Bayes criterion
Expected Strategies E(Di) =
S Pi Rij (profit incurred under jth market situation at ith level of yield
Max (E(Di)) = Max (average payoffs)
Select the action alternative with the best E (Si) as the optimal decision. “Best” means max for positive payoffs (profits, revenues) and min for negative payoffs (costs).
RESULTS AND DISCUSSION
A farmer from Kadapa district who followed multiple cropping systems is selected at random and collected data from him. Data contains the cost of cultivation, yields and market prices pertaining to six crops; groundnut, paddy, sunflower, red gram, cotton and sesame cultivated by him. profits for each crop under four different situations viz., good yield with high market price; good yield with low market price; poor yield with high market price; and poor yield with low market price are calculated. He faced many challenges with fluctuated prices and uncertain yields due to many uncontrollable factors.
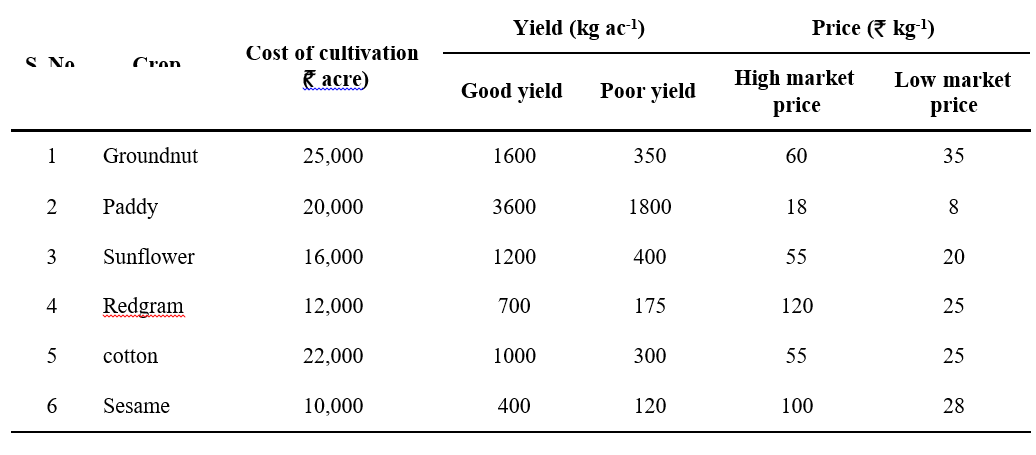
Cost of Cultivation Matrix
Profit matrix
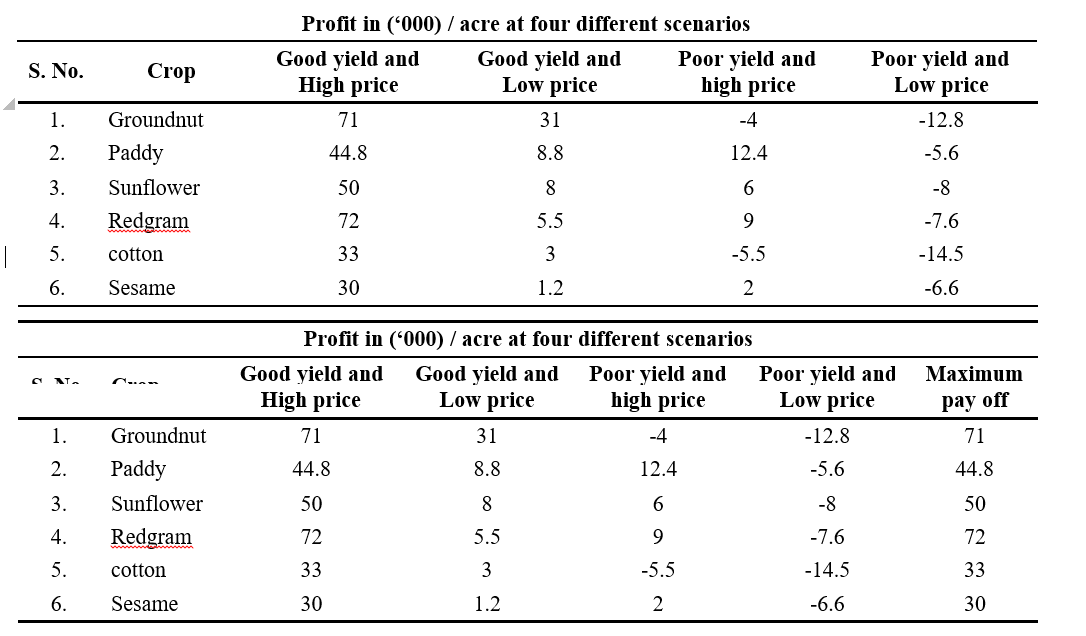
Maximax criterion = Max (Maximum payoff)
= Max (71.0, 44.8, 50.0, 72.0, 33.0, 30.0)
= 72.0 (Redgram)
Maximin criterion
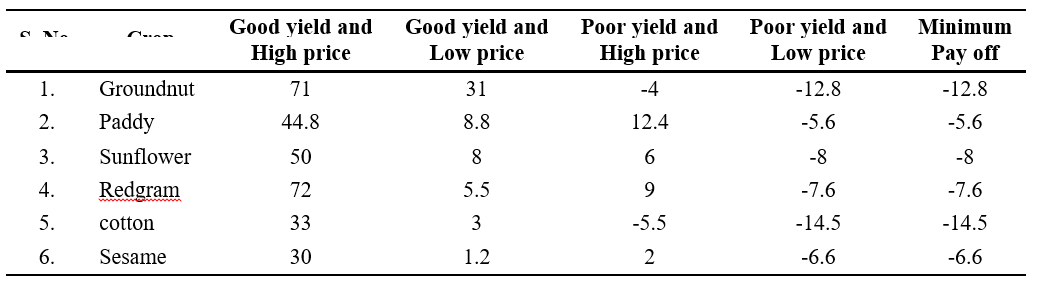
Profit in (‘000) / acre at four different scenarios
Maximin criterion = Max (Minimum payoff)
= Max (-12.8, -5.6, -8.0,-7.6, -14.5, -6.6)
= -5.6 (paddy)
Hurwicz’s criterion
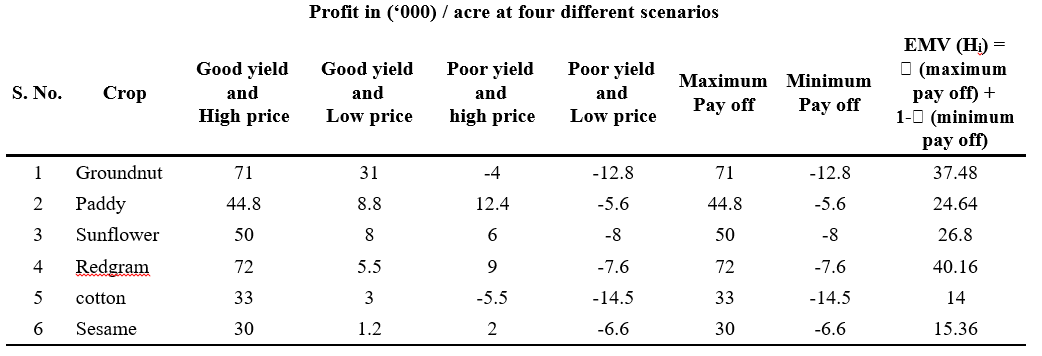
Generally a value lies between 0 to 1 with the intention of maximising the profit I have taken a = 0.6 E.M.V (Hi)
=a (maximum pay off) + 1-a (minimum pay off)
Minimax regret criterion Redgram = 40.16 Laplace criterion
Regrets = maximum payoff – payoff Minmax regrets = min(maximum regrets)
= min (83.8, 50.4, 58, 79.6, 47.5, 36.6)
= 36.6 (sesame)
Laplace criterion
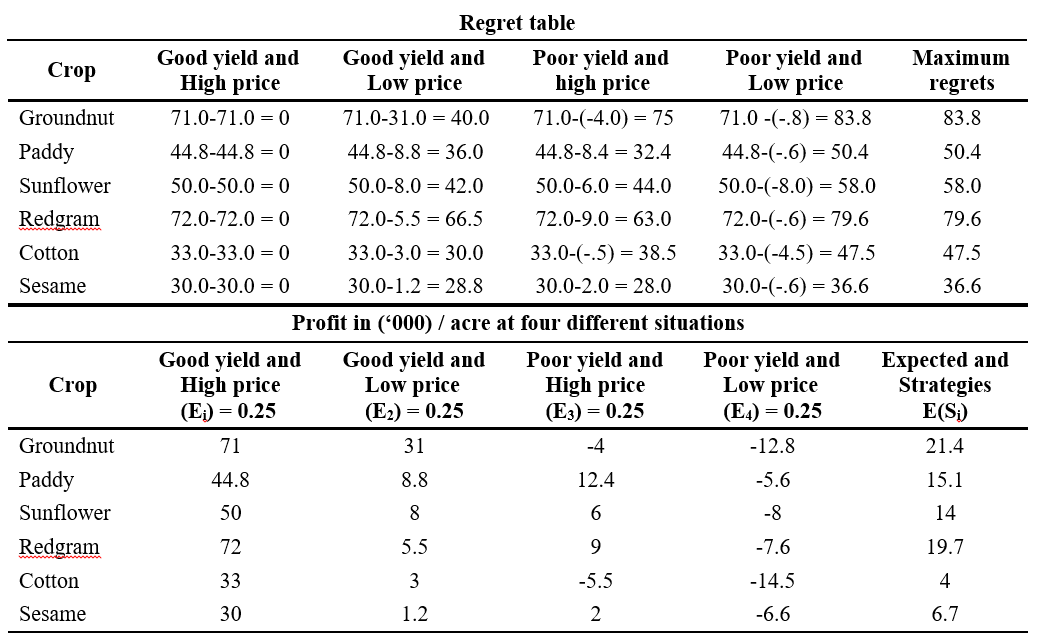
Expected Strategies E(Si) = S Pi Rij (profit incurred under jth market situation at ith level of yield)
Max (E(Si) = Max (21.4, 15.1, 14.0, 19.7, 4.0, 6.7)
= 21.4 ( Groundnut)
From the study I have drawn these conclusions which optimise the farmer’s profit in view of his nature from different methodologies taken.
- If the farmer is optimistic, Redgram is a better option
- The suitable crop for the pessimistic farmer is
Paddy.
- Redgram is the better choice for the farmer who is neither optimistic nor pessimistic with (0.6 weightage for optimism and 0.4 weightage for pessimism) the intention of maximum
- Sesame is the best alternative if he accounts for opportunity loss as a risk avert from his previous
- If there is equal chance for happening of any one of the four alternatives in the coming season the best choice for him (risk bearer) is Groundnut to achieve optimum profits even the production and market price is not
LITERATURE CITED
Ahuja, H.L. 2010. Advanced Microeconomic Analysis, 17th edition. S. Chand and Company Ltd.
Bavec, F and Bavec, M. 2006. Organic production and use of alternative crops, (Books in soils, plants, and the environment, 116). Boca Raton; New York; London: Taylor & Francis: CRC Press, 241.
Bowden, R.J., Ison, R.L., Mecadm, R.D., Packham, R.G and Valentin, I. 1985. Research paradigm for systems agriculture. Proceedings of an International Workshop held at Howkesburg Agricultural College, Richmand, N.S.W, (Australia), 65.
Frank, A and Ragnar, T. 1999. Modeling production risk with a two-step procedure. Journal of Agricultural and Resource Economics. 24(2): 424-439.
Kumari, P.L., Reddy, G.K and Krishna, T.G. 2014. Optimum allocation of agricultural land to the vegetable crops under uncertain profits using fuzzy multi objective linear programming. IOSR Journal of Agriculture and Veterinary Science. 7(12): 19-28.
Nieuwoudt, W.L. 1972. Risk and uncertainty in agriculture. Agricultural Economics Research, Policy and Practice in Southern Africa. 11(2): 20-25.
Robson, M.C., Fower, S.M., Lampkin, N.H., Leifert, C., Leitch, M., Robinson, D., Watson, C.A and Litterick,
A.M. 2002. The agronomic and economic potential of break crops for ley/arable rotations in temperate organic agriculture. Advances in Agronomy. 77: 369- 427.
Rozman, È., Pažek, K., Bavec, M., Bavec, F., Turk, J and Majkoviè, D. 2006: The Multi-criteria analysis of spelt food processing alternatives on small organic farms. International Journal of Agricultural Sustainability. 28(2):159-179.
Sahin, A., Miran, B., Yildirim, I and Onenc, A. 2008. Profit maximization of cattle fattening breed based on characteristics of producers: An application of game theory. Journal of Animal and Veterinary Advances. 7(10): 1305-1309.
Raju, K.S and Kumar, D.N. 2000. Optimum cropping pattern for Sri Ram Sagar Project: A linear programming approach. Journal of Applied Hydrology. 8: 57-67.
- Genetic Diversity Analysis of 64 Maize Inbred Lines for Yield Traits Using D2 Statistics and Principal Component Analysis
- Effect of Border Crops on Activity of Predatory Fauna In Blackgram (Vigna Mungo L.)
- Effect of Organic Nutrient Management Practices on Growth and Yield of Foxtail Millet
- Species Diversity of Sugarcane Shootborers in Major Sugarcane Growing Districts of Andhra Pradesh
- Faunistic Studies on Economically Important Lepidopterans in Different Field Crops of Tirupati District
- Production Potential of Sweet Corn as Influenced by Organic Manures and Foliar Nutrition

